杂记
- 机器学习致力于研究如何通过计算的手段,利用经验来改善系统自身的性能。
- 机器学习所研究的内容,是关于在计算机上从数据中产生“模型”的算法,即“学习算法”。
- 学得模型适用于新样本的能力,称为泛化能力。
- 归纳和演绎是科学推理的两大基本手段。前者是从特殊到一般的泛化过程,即从具体事实归结出一般性规律;后者是从一般到特殊的特化过程,即从基础原理推演出具体状况。“从样本中学习”显然是一个归纳过程,因此亦称为“归纳学习”。归纳学习有广义与狭义之分,广义大体相当于从样本中学习;狭义则要求从样本中学得概念,因此也称为“概念学习”或“概念形成”。但当下现实中常用的技术大多是黑箱模型。
- 任何一个有效的机器学习算法必然有其归纳偏好,否则如果假设空间中存在多个假设都与训练集一致,算法无法得出固定的结论。
- 存在一个一般性的原则来引导算法确立“正确的”偏好,“奥卡姆”剃刀是一种常用的、自然科学研究中最基本的原则,即“若有多个假设与观察一致,则选最简单的那个”。
- 机器学习分为两类:
- 符号主义:包括决策树和基于逻辑的学习,能产生明确的概念
- 连接主义:神经网络,模型是一个黑箱
概念
凸集
实数$\mathbb{R}$或复数$\mathbb{C}$向量空间中,集合$S$称为凸集,当且仅当$S$中任意两点的连线上的点也在集合$S$内,因为只有这样,集合的外形才是凸的,没有凹进去的部分,才叫做凸集。
换成严谨的数学定义就是:对于集合$S$以及集合内的任意两点$x, y$,如果对$\forall \alpha \in [0, 1]$,都有$\alpha x + (1 - \alpha)y \in S$,那就称集合是一个凸集。
距离
对于点$X(x_1, x_2)$和点$Y(y_1, y_2)$
- 欧氏距离
- 曼哈顿距离
- 闵可夫斯基距离
- 余弦相似度
余弦相似度考察两个向量在空间中方向的接近程度,若$\cos \theta$很小,则可以将两个点视为一个聚类簇中。
混淆矩阵
| 真实情况\预测结果 | 正 | 反 |
|---|---|---|
| 正 | TP | FN |
| 反 | FP | TN |
- 查准率
- 查全率或召回率
P-R图
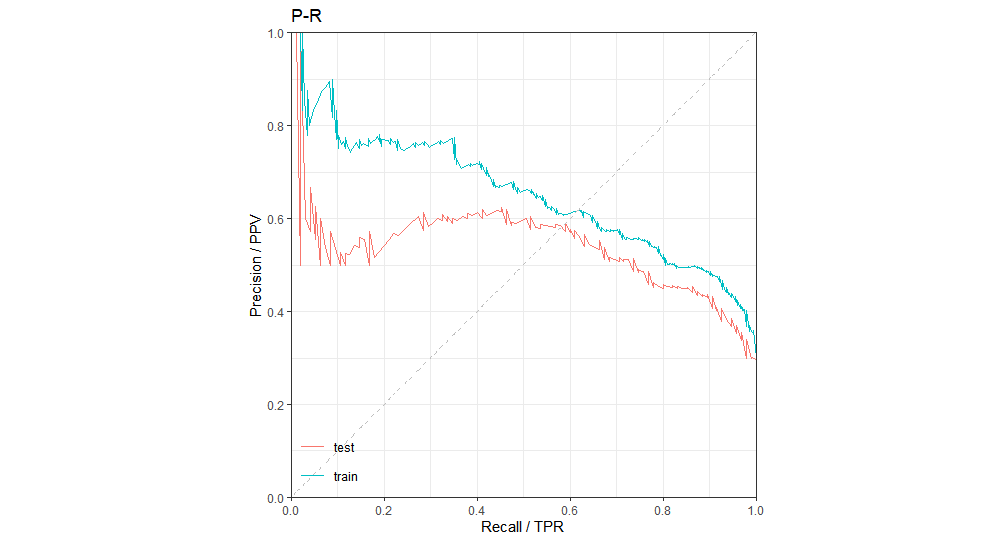
其中曲线与对角线的交点为Precision-Recall平衡点,PPV全称为Positive Predictive Value。对于样本中数据类型不平衡的情况,P-R曲线受特定数据集影响较大,因为查准率会受影响,而ROC曲线比较稳定。
由查准率和查全率可以计算$F_1$指标:
\[F_1 = \frac {2P \cdot R} {P + R}\]对于$F_1$来说,越大学习器性能越好。
ROC图
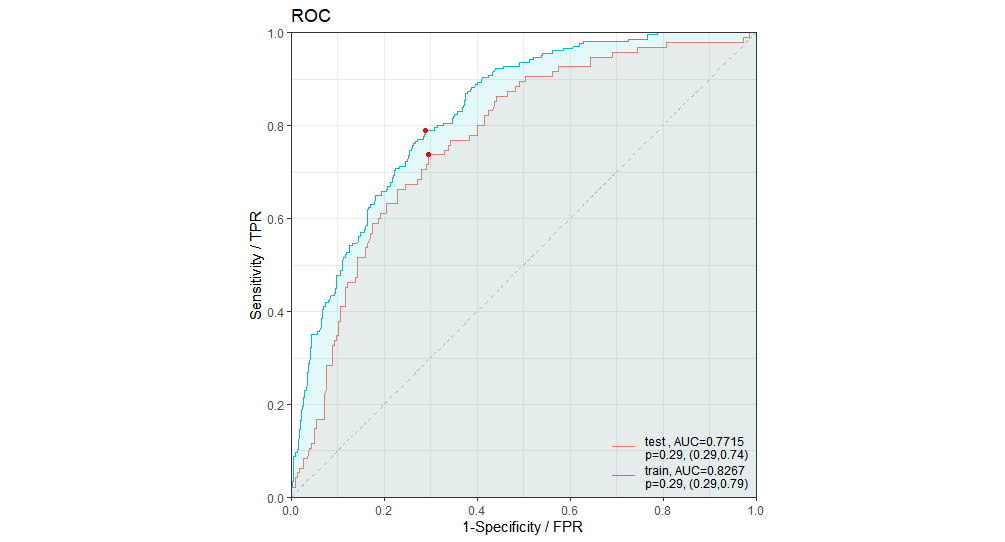
- 真阳性率(True Positive Rate)
- 假阳性率(False Positive Rate)
ROC曲线下的面积大小为AUC,取值范围为$[0.5, 1]$,因为如果一个学习器的AUC小于0.5,还不如扔硬币来猜,这样还会有50%的概率正确。
过拟合
过拟合指模型在训练时拟合程度过当的情况,模型过度学习某个样本的噪声与细节,表现为在训练集上的拟合效果很好,但更换数据集后拟合效果很差。
- 降低过拟合:增加样本量,降低模型复杂度
- 降低欠拟合:增加新的特征,增加模型复杂度
方差偏差权衡
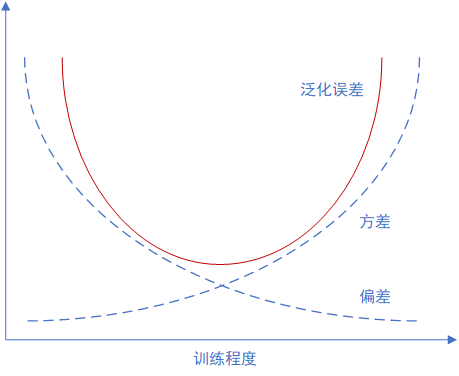
当学习器训练不足时,学习器拟合能力不足,偏差主导泛化误差,随着训练程度的加深,方差主导泛化误差。






