选择排序

1. 首先在未排序序列中找到最小（大）元素，存放在排序序列的起始
2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放在已排序序列末尾
3. 重复步骤2

选择排序是遍历比较的，不同于冒泡法在每次比较后会交换元素位置，选择排序只记录本次遍历中最小（大）值角标。

冒泡排序

1. 比较相邻的元素，如果第一个比第二个大，就交换它们
2. 对每一对相邻元素做同样工作，从开始一对至最后一对，这步做完后，最后的元素会是最大值
3. 针对所有元素重复步骤2，除了最后一个元素
4. 持续重复步骤2和3

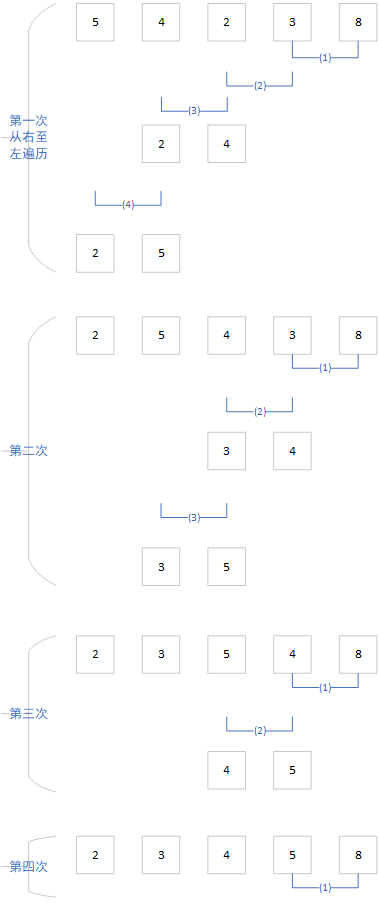
像鱼吐泡泡一样，每次由右至左（或由左至右）遍历，故称冒泡法，且具有两层循环，故时间复杂度为$O(n^2)$。

插入排序

1. 将第一待排序列第一个元素看作一个有序序列，把第二个元素到最后一个元素当作未排序序列
2. 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置（如果待插入的元素与有序序列中某个元素相等，则将待插入元素插入相等元素的后面）

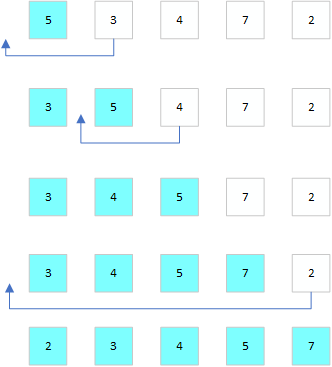
未排序序列中有一层循环，已排序序列中有一层循环，故时间复杂度是$O(n^2)$。

快速排序

1. i向右寻找比基准数大的数，j向左寻找比基准数小的数，j必须先行
2. j找到数后，i开始寻找，i找到后，i与j指向的数交换
3. 继续，当i和j相遇时，将基准数与此时位置交换
4. 左右两侧分别重复步骤1、2、3

def quick_sort(array, l, r):
    if l < r:
        q = partition(array, l, r)
        quick_sort(array, l, q - 1)
        quick_sort(array, q + 1, r)


def partition(array, l, r):
    x = array[r]
    i = l - 1
    for j in range(l, r):
        if array[j] <= x:
            i += 1
            array[i], array[j] = array[j], array[i]
    array[i+1], array[r] = array[r], array[i+1]
    return i+1