在数据分析过程中,一个完整的闭环是从数据中得到洞察,根据洞察得到某种假设,通过实验检验这一假设。直观上看,进行实验的样本量越大越好,因为较小的样本量容易使实验结果被新的样本点改变,造成结果的不稳定。但实际中,流量有限、试错成本大使得进行实验使用的样本量越少越好,因此如何确定合适的样本量是一个关键问题。
ABTest主要涉及假设检验中的两种,一种应用于均值,一种应用于比率。
均值
对于业务来说,某个指标的提升只有达到一定数额之后才会被视为具有业务意义。因此对于测试组A和对照组B,我们想验证的是实验是否将均值显著提高了$\delta$,也就是有下面的假设
\[H_0: \mu_A - \mu_B \le \delta \\ H_1: \mu_A - \mu_B > \delta\]同时我们令
\[\kappa = \frac {n_A} {n_B}\]我们以总体方差已知为例,因为测试组和对照组相互独立并来自同一总体,因此它们的总体方差一定相等,假定总体服从正态分布,于是使用如下的检验统计量
\[z = \frac {(\bar X_A - \bar X_B) - (\mu_A - \mu_B)} {\sigma \sqrt {\frac 1 {n_A} + \frac 1 {n_B}}} \sim N(0, 1)\]根据第一类错误和第二类错误的定义,绘制图形如下
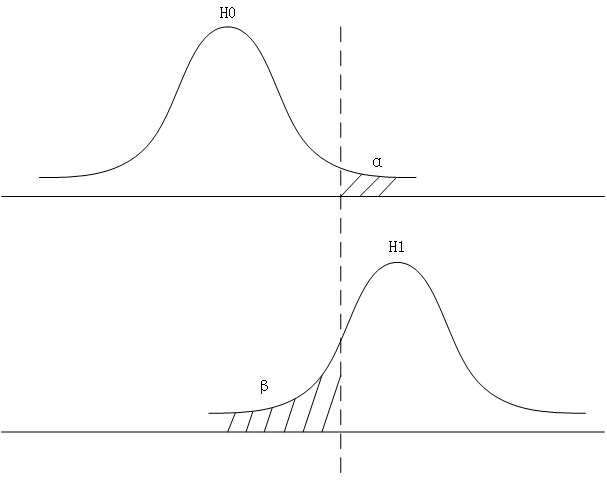
第二类错误即取伪,当H0为假时,样本实际来自H1总体,但在H0上的假设检验错误地没有拒绝原假设,造成了第二类错误。对于第二类错误$\beta$有如下的计算公式
\[\begin{aligned} \beta &= P(接受H_0 \vert H_0为假) \\ &= P(\frac {(\bar X_A - \bar X_B) - \delta} {\sigma \sqrt {\frac 1 {n_A} + \frac 1 {n_B}}} \le z_{\alpha} \vert H_0为假) \\ &= P(\frac {(\bar X_A - \bar X_B) - (\mu_A - \mu_B)} {\sigma \sqrt {\frac 1 {n_A} + \frac 1 {n_B}}} \le z_{\alpha} - \frac {\mu_A - \mu_B - \delta} {\sigma \sqrt {\frac 1 {n_A} + \frac 1 {n_B}}}) \\ &= \Phi(z_{\alpha} - \frac {\mu_A - \mu_B - \delta} {\sigma \sqrt {\frac 1 {n_A} + \frac 1 {n_B}}}) \\ &= \Phi(- z_{\beta}) \end{aligned}\]满足给定$\alpha, \beta$下的最小样本量在下面等式中取到
\[z_{\alpha} - \frac {\mu_A - \mu_B - \delta} {\sigma \sqrt {\frac 1 {n_A} + \frac 1 {n_B}}} = - z_{\beta}\]于是就有
\[n_A = \kappa n_B \\ n_B = (1 + \frac 1 \kappa)(\sigma \frac {z_{\alpha} + z_{\beta}} {\mu_A - \mu_B - \delta})^2\]由上面的公式即可推出两个分组各自的样本量大小。对于假设
\[H_0: \mu_A - \mu_B \le 0.01 \\ H_1: \mu_A - \mu_B > 0.01\]设定显著性水平为5%,统计功效为80%,$\kappa = 1$,由公式推导得出样本量为
from scipy.stats import norm
def compute(mu_a, mu_b, delta, sigma, k, alpha, beta):
n_b = (1 + 1 / k) * (sigma * (norm.ppf(1 - alpha) + norm.ppf(1 - beta)) / (mu_a - mu_b - delta)) ** 2
n_a = k * n_b
return n_a, n_b
print(compute(0.45, 0.4, 0.01, 1, 1, 0.05, 0.2))
# >>> (7728.196540024712, 7728.196540024712)
求解方法在python中有现有库可使用
from statsmodels.stats.power import zt_ind_solve_power
zt_ind_solve_power(
effect_size=(.45 - .4 - 0.01) / 1,
alpha=0.05,
power=0.8,
ratio=1,
alternative='larger'
)
# >>> 7728.196540024726
上面求解得到的是$n_A$的值,其中使用到了一个参数“效应量”。
效应量是一个统计概念,它在数字尺度上衡量两个变量之间关系的强度。例如,如果我们有关于男性和女性身高的数据,并且我们注意到,平均而言,男性比女性高,男性身高和女性身高之间的差异被称为效应量。效应量越大,男女身高差越大。统计效应量帮助我们确定差异是真实的还是由于因素的变化。在假设检验中,效应量、统计功效、样本量和显著性水平彼此相关。在统计分析中,效应大小通常以三种方式衡量:
- 标准均差(standardized mean difference)
- 几率(odd ratio)
- 相关系数(correlation coefficient)
我们使用标准均差效应量即可
\[\theta = \frac {\mu_1 - \mu_2} \sigma\]比率
对于像转化率这类比率型指标,有如下假设
\[H_0: \pi_A - \pi_B \le \delta \\ H_1: \pi_A - \pi_B > \delta\]同时令
\[\kappa = \frac {n_A} {n_B}\]使用如下检验统计量
\[z = \frac {(p_A - p_B) - (\pi_A - \pi_B)} {\sqrt {\frac {p_A(1-p_A)} {n_A} + \frac {p_B(1-p_B)} {n_B}}} \sim N(0, 1)\]与均值类的推导过程类似,有
\[n_A = \kappa n_B \\ n_B = (\frac {p_A(1 - p_A)} \kappa + p_B(1 - p_B))(\frac {z_{\alpha} + z_{\beta}} {\pi_A - \pi_B - \delta})^2\]由上面的公式即可推出两个分组各自的样本量大小。对于假设
\[H_0: \pi_A - \pi_B \le 0.05 \\ H_1: \pi_A - \pi_B > 0.05\]设定显著性水平为5%,统计功效为80%,$\kappa = 1$,由公式推导得出样本量为
from scipy.stats import norm
def compute(p_a, p_b, delta, k, alpha, beta):
n_b = ((p_a * (1 - p_a) / k) + p_b * (1 - p_b)) * ((norm.ppf(1 - alpha) + norm.ppf(1 - beta)) / (p_a - p_b - delta)) ** 2
n_a = k * n_b
return n_a, n_b
print(compute(0.5, 0.4, 0.05, 1, 0.05, 0.2))
# >>> (1211.7812174758753, 1211.7812174758753)
我们使用Cohen’s h效应量
\[h = 2 \times (arcsin(\sqrt {p_A}) - arcsin(\sqrt {p_B}))\]from statsmodels.stats.power import zt_ind_solve_power
import numpy as np
zt_ind_solve_power(
effect_size=2 * (np.arcsin(np.sqrt(0.5)) - np.arcsin(np.sqrt(0.4)) - 0.05),
alpha=0.05,
power=0.8,
ratio=1,
alternative='larger'
)
# >>> 1203.6015972559796






