统计量
设$X_1, …, X_n$是从总体$X$中抽样的样本,如果由此样本构造一个不依赖任何未知参数的函数$T(X_1, …, X_n)$,则称函数$T$是一个统计量。
样本均值
\[\bar{X} = \frac{1}{n} \sum X_i\]样本方差
\[s^2 = \frac{1}{n-1} \sum (X_i - \bar{X})^2\]变异系数
\[CV = \frac{s}{\bar{X}}\]样本标准差除以样本均值。当比较两组不同量纲数据的离散程度时,直接用标准差比较不合适,应该消除量纲的影响。
异众比率
\[V_r = 1 - \frac{f_m}{\sum f_i}\]其中$f_m$是众数组的频数,$\sum f_i$是总频数。
k阶原点矩
\[m_k = \frac{1}{n} \sum X^k_i\]k阶中心距
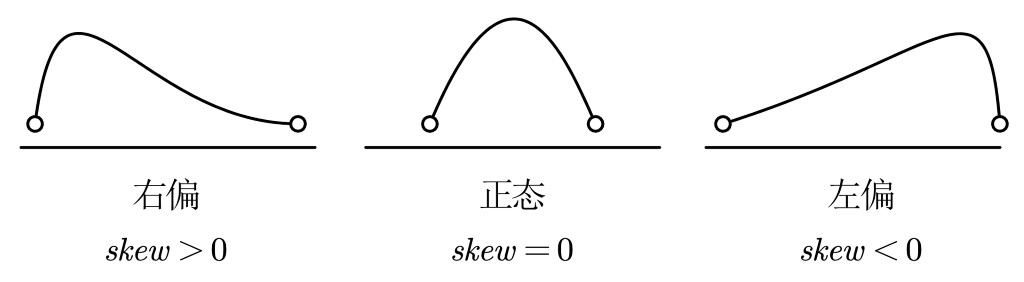
\[v_k = \frac{1}{n-1} \sum (X_i - \bar{X})^k\]偏度
\[skew = E[(\frac{X - \mu}{\sigma})^3]\]即3阶中心距。
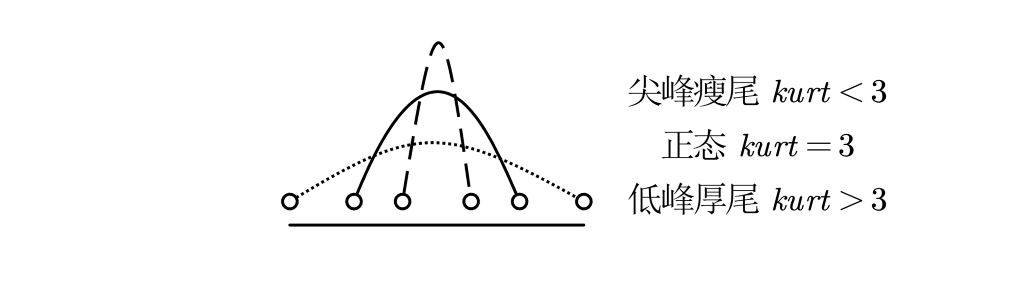
峰度
\[kurt = E[(\frac{X - \mu}{\sigma})^4]\]即4阶中心距。
分布
二项分布
\[B(n, p) \\ EX = np, DX = np(1 - p)\]泊松分布
\[P(x) = \frac{\lambda^x e^{-\lambda}}{x!}, x = 0, 1, 2, ... \\ EX = \lambda, DX = \lambda\]正态分布
\[f(x) = \frac 1 {\sqrt{2\pi} \sigma} e^{-\frac{(x - \mu)^2}{2 \sigma^2}}, x \in \mathbb{R} \\ EX = \mu, DX = \sigma^2\]指数分布
\[f(x) = \begin{cases} \lambda e^{-\lambda x}, x>0 \\ 0, x \le 0 \end{cases}\]或
\[f(x) = \begin{cases} \frac 1 \theta e^{-\frac x \theta}, x>0 \\ 0, x \le 0 \end{cases} \quad \theta = \frac 1 \lambda\] \[F(x) = \begin{cases} 1 - e^{-\lambda x}, x>0 \\ 0, x \le 0 \end{cases}\] \[EX = \frac 1 \lambda, DX = \frac 1 {\lambda^2}\]卡方分布
若$X_1, …, X_n$相互独立,且$X_i \sim N(0, 1)$,则
\[\sum^n_{i=1} X^2_i \sim \chi^2 (n) \\ EX = n, DX = 2n\]t分布
\[EX = 0, DX = \frac n {n - 2}\]若$X \sim N(0, 1)$,$Y \sim \chi^2(n)$,$X$与$Y$相互独立,则
\[t = \frac X {\sqrt{\frac Y n}}\]若$X \sim N(\mu, \sigma^2)$,则
\[\bar X = \frac 1 n \sum^n_{i=1} X_i \\ E \bar X = \frac 1 n \sum EX_i = \mu \\ D \bar X = \frac 1 {n^2} \sum DX_i = \frac {\sigma^2} n\]因此:
\[\frac {\bar X - \mu}{\frac \sigma {\sqrt n}} \sim N(0, 1)\]又有如下的推导存在:
\[s^2 = \frac 1 {n - 1} \sum^n_{i=1} (X_i - \bar X)^2 \\ \begin{aligned} \frac {(n-1)s^2}{\sigma^2} &= \frac {\sum(X_i - \bar X)^2}{\sigma^2} = \sum (\frac{X_i}{\sigma} - \frac{\bar X}{\sigma})^2 \\ &= \sum (\frac{X_i - \mu}{\sigma} - \frac{\bar X - \mu}{\sigma})^2 \\ &= \sum (Z_i - \bar Z)^2 \\ &= \sum (Z_i^2 - 2Z_i \bar Z + \bar Z^2) \\ &= \sum^n_{i=1} Z^2_i - n\bar Z^2 \sim \chi^2(n - 1) \end{aligned}\]故
\[\frac {\frac {\sqrt n (\bar X - \mu)} \sigma} {\sqrt{\frac{\frac{(n-1)s^2}{\sigma^2}}{n - 1}}} = \frac {\sqrt n (\bar X - \mu)} s \sim t(n-1)\]F分布
若$Y$与$Z$相互独立,$Y \sim \chi^2(m)$,$Z \sim \chi^2(n)$,则
\[X = \frac {\frac Y m}{\frac Z m} \sim F(m, n) \\ EX = \frac n {n - 2} \\ DX = \frac {2 n^2(m+n-2)} {m(n-2)(n-4)}, n>4\]定理
极限定理是概率论的基本理论,在理论研究和应用中起着重要的作用,其中最重要的是称为“大数定理”和“中心极限定理”的一些定理。大数定理是叙述随机变量序列的前一些项的算术平均值在某种条件下收敛到这些项的均值;中心极限定理则是确定在什么条件下,大量随机变量之和的分布逼近于正态分布。
切比雪夫不等式
设随机变量$X$具有期望$E(X) = \mu$,方差$D(X) = \sigma^2$,则对于任意$\varepsilon > 0$,下面的不等式成立:
\[P(\mid X - \mu \mid \ge \varepsilon) \le \frac {\sigma^2} {\varepsilon^2}\]证明:
设$X$的概率密度函数为$f(x)$,则有
\[\begin{aligned} P(\mid X - \mu \mid \ge \varepsilon) &= \int_{\mid x - \mu \mid \ge \varepsilon} f(x) dx \le \int_{\mid x - \mu \mid \ge \varepsilon} \frac {\mid x - \mu \mid^2} {\varepsilon^2}f(x) dx \\ &\le \frac 1 {\varepsilon^2} \int_{-\infty}^{\infty} (x- \mu)^2f(x)dx = \frac {\sigma^2} {\varepsilon^2} \end{aligned}\]切比雪夫不等式也可以写成下面的形式:
\[P(\mid X - \mu \mid < \varepsilon) \ge 1 - \frac {\sigma^2} {\varepsilon^2}\]切比雪夫不等式给出了在随机变量分布未知,但已知期望方差时,估计概率$P(\mid X - EX \mid < \varepsilon)$的界限。
大数定理
弱大数定理(辛钦大数定理)
设$X_1, X_2, …$相互独立、服从同一分布的随机变量序列,且具有数据期望$E(X_k)=\mu (k=1,2,…)$。前n个变量的算术平均为$\frac 1 n \sum_{k=1}^n X_k$,则对于任意$\varepsilon>0$,有
\[\lim_{n \to \infty} P\{\mid \frac 1 n \sum_{k=1}^n X_k - \mu \mid < \varepsilon \} = 1\]也称序列$\bar X = \frac 1 n \sum_{k=1}^n X_k$依概率收敛于$\mu$,即$\bar X \xrightarrow{P} \mu$。
证明:
在随机变量的方差存在情况下证明。因为:
\[E(\frac 1 n \sum_{k=1}^n X_k) = \frac 1 n \sum_{k=1}^nE(X_k)=\frac 1 n (n\mu) = \mu\]又由独立性得:
\[D(\frac 1 n \sum_{k=1}^n X_k) = \frac 1 {n^2} \sum_{k=1}^nD(X_k)=\frac 1 {n^2} (n\sigma^2) = \frac {\sigma^2} n\]由切比雪夫不等式得:
\[1 \ge P\{\mid \frac 1 n \sum_{k=1}^n X_k - \mu \mid < \varepsilon \} \ge 1 - \frac {\frac {\sigma^2} n} {\varepsilon^2}\]在上式中令$n \to \infty$,即得:
\[\lim_{n \to \infty} P\{\mid \frac 1 n \sum_{k=1}^n X_k - \mu \mid < \varepsilon \} = 1\]伯努利大数定理
设$f_A$是$n$次独立重复试验中事件A发生的次数,$p$是事件A在每次试验中发生的概率,则对于任意$\varepsilon > 0$,有
\[\lim_{n \to \infty} P(\mid \frac {f_A} n - p \mid < \varepsilon) = 1\]或
\[\lim_{n \to \infty} P(\mid \frac {f_A} n - p \mid \ge \varepsilon) = 0\]这即是频率稳定性的真正含义,当试验次数很大时,便可以用事件的频率来代替概率。
中心极限定理
独立同分布的中心极限定理
设随机变量$X_1, X_2, …, X_n$ i.i.d,$E(X_k) = \mu$,$D(X_k) = \sigma^2 > 0$,则随机变量之和$\sum_{k=1}^n X_k$的标准化变量
\[Y_n = \frac {\sum_{k=1}^n X_k - E(\sum_{k=1}^n X_k)} {\sqrt {D(\sum_{k=1}^n X_k)}} = \frac {\sum_{k=1}^n X_k - n\mu} {\sqrt n \sigma}\]的分布函数$F_n(x)$对于任意$x$满足
\[\begin{aligned} \lim_{n \to \infty} F_n(x) &= \lim_{n \to \infty} P(\frac {\sum_{k=1}^n X_k - n\mu} {\sqrt n \sigma} \le x) \\ &= \int_{-\infty}^x \frac 1 {\sqrt {2\pi}} e^{- \frac {t^2} {2}} dt = \Phi(x) \end{aligned}\]一般情况下,很难求出$n$个随机变量之和的分布函数,上式表明当$n$充分大时,可以用正态分布来近似。上面公式的另一个形式为:
\[\frac {\sum_{k=1}^n X_k - n\mu} {\sqrt n \sigma} = \frac {\frac 1 n \sum_{k=1}^n X_k - \mu} {\sigma / \sqrt n} \overset{近似地}{\sim} N(0, 1) \\ \frac 1 n \sum_{k=1}^n X_k \overset{近似地}{\sim} N(\mu, \sigma^2 / n)\]李雅普诺夫(Lyapunov)定理
设随机变量$X_1, X_2, …, X_n$相互独立,$E(X_k) = \mu_k$,$D(X_k) = \sigma_k^2 > 0$,记$B_n^2 = \sum_{k=1}^n \sigma_k^2$,若存在$\delta > 0$,使得当$n \to \infty$时
\[\frac 1 {B_n^{2 + \delta}} \sum_{k=1}^n E(\mid X_k - \mu_k \mid ^{2+\delta}) \to 0\]则随机变量之和$\sum_{k=1}^n X_k$的标准化变量
\[Z_n = \frac {\sum_{k=1}^n X_k - E(\sum_{k=1}^n X_k)} {\sqrt {D(\sum_{k=1}^n X_k)}} = \frac {\sum_{k=1}^n X_k - \sum_{k=1}^n \mu_k} {B_n}\]的分布函数$F_n(x)$对于任意$x$满足
\[\begin{aligned} \lim_{n \to \infty} F_n(x) &= \lim_{n \to \infty} P(\frac {\sum_{k=1}^n X_k - \sum_{k=1}^n \mu_k} {B_n} \le x) \\ &= \int_{-\infty}^x \frac 1 {\sqrt {2\pi}} e^{- \frac {t^2} {2}} dt = \Phi(x) \end{aligned}\]也就是说,无论各个随机变量服从什么分布,只要它们相互独立,满足期望存在方差有限,当$n$无穷大时,它们的和就近似服从正态分布。
棣莫弗-拉普拉斯定理
设随机变量$\eta_n$服从参数为$n, p (0 < p < 1)$的二项分布,则对于任意$x$有
\[\lim_{n \to \infty} P(\frac {\eta_n - np} {\sqrt{np(1-p)}} \le x) = \int_{-\infty}^x \frac 1 {\sqrt {2\pi}} e^{- \frac {t^2} 2} dt = \Phi(x)\]这个定理表明,正态分布是二项分布的极限分布。






