辛普森悖论为英国统计学家E.H.辛普森（E.H.Simpson）于1951年提出的悖论，即在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论。

以一个经典的例子来说明：一个大学有商学院和法学院两个学院，某次招生结束后，被外界批评存在性别歧视，招收的男生录取率比女生高。下图为两个学院的汇总数据：

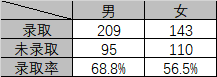
从汇总数据来看，男生的录取率比女生高，但实际在每个学院中，女生的录取率比男生要高，如下图所示：

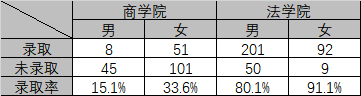
分组讨论时得出的结论与汇总时得出的结论相悖。在该例中，女生申请商学院的人数占比为60%，申请法学院的占比为40%；男生申请商学院的人数占比为17%，申请法学院的占比为83%。同时商学院的总录取率为28.78%，法学院的总录取率为83.24%。结果从数量上来看，录取率较低的商学院因为申请的女生多，所以未录取的女生多；录取率较高的法学院因为申请的男生多，所以录取的男生多。使得在汇总时，男生在数量上占优势。

误区产生的原因在于：

• 两个学院的录取率相差很大，但两种性别的申请者分布比重却正好相反；
• 性别并非是录取率高低的唯一因素，甚至可能毫无影响，产生这种现象可能是随机事件。

想要避免辛普森悖论带来的数据陷阱，就需要给分组加上一定权重来消除分组资料基数差异所造成的影响。譬如，产品转化率分析时就需要拆分为免费用户ARPU（Average Revenue Per User）和付费用户ARPPU（Average Revenue Per Paying User），因为大多数用户都是不付费的，将所有用户汇总在一起看，任何对免费用户的衡量都是非常低的。

在做ABTest时，一个易犯的错误是拿1%的用户跑了一个重大版本，发现实验版本转化率比对照组高，就得出结论说测试组更好，应该立即发布。而事实上，我们选取的测试组很有可能会挑选那些用户粘性高、热衷于使用产品的用户，把它们的数据与全体用户对比是不客观的。当最后发布测试版本时，反而可能会降低用户体验，造成用户留存和转化双双下降。

避免辛普森悖论的关键在于不要用部分属性数据当做全属性数据的结果，在一个具体的数据分析中，汇总的数据对比往往没有多大的参考意义，一定要细分到具体再进行对比才有价值。