我们需要认识到信用评分的发展是以风险评量为出发点，为求主题明确，聚焦于风险因子的探讨，收益面并非考虑重点。因此，风险极低者未必是获利贡献度最高的客户。同时，信用评分模型以“户数”为单位计算好坏比，我们可借此得知各分数下可能逾期的户数比率，而一般评估风险所惯用的逾期比率则是以“金额”为计算单位，两者计算基础不同，户数逾期率与金额逾期率无法相互比较。
根据使用时机，可以将信用评分卡分为三类：
- 申请评分（Application Score）
- 行为评分（Behavior Score）
- 催收评分（Collection Score）
基本定义
观察期与表现期
观察期即为变量计算的历史区间。比如，有一变量为“近6个月逾期一期以上（M1+）的次数”，其观察期就等于6个月。观察期设定太长，可能无法反映近期状况，设定太短则稳定性不高，因此多半为6~24个月。
表现期则是准备预测的时间长度。例如，若想要预测客户未来12个月内违约的概率，则表现期为12个月。根据各种产品特性不同，表现期可能不同，通常设定为12~24个月。
违约（Bad）定义
评分模型的任务在于区隔好坏客户，因此必须定义违约条件，这些条件并不限定为逾期，只要认定此情况为“非目标客户”。
不确定定义
在某些条件下的客户，其风险处于较为模糊的灰色地带，很难将其归为好客户或坏客户。为强化模型的区隔能力，不确定的客户不适合被纳入建模样本中，不过在模型完成后可加入测试，观察其分数落点，理论上应以中等分数居多。在实际应用中，可利用转移分析（Roll Rate Analysis）观察各条件下的客户经过一段时间后的表现，以评估违约定义的区隔能力与稳定度，作为其选择好坏及不确定条件的参考。
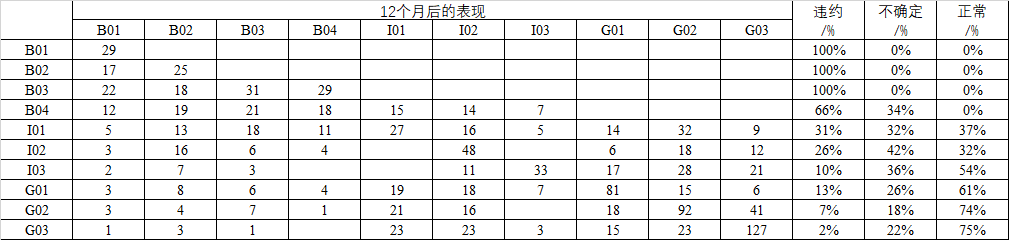
上表中B表示违约定义，I表示不确定定义，G表现正常定义。经过12个月的观察，原违约者大多数停留在违约状态，而原正常者转坏的比例也不高，这表示好坏客户的定义可被接受。原I03客户在12个月后明显往正常方向移动，因此可考虑将其改入正常定义组。
评分范围
虽然信用评分可快速预测潜在风险，但并非所有状况都必须依赖评分来判断风险。如数据遗漏严重、数据期间过短和近来无信用往来记录者等状况的出现使这些客户的信息不足，对其评分也没有太大意义。
样本分组
为了获得最佳的预测效果，通常可以根据客群或产品特性做样本分组，分别开发评分卡。若受限于时间，权宜之计为共享一张评分卡的同时调整不同应用场景下的准驳临界点，不过效果可能较差。适度的样本分组有助于提高模型的预测效果，不过要避免过度使用，如果切割过细，不但后续评分卡维护困难，且建模样本不足反而会影响模型的预测能力与稳定性。
变量分析
变量的形态可分为连续变量和离散变量。首先，从所有数据中挑选或组合出可能影响风险的变量，这些一开始先挑出的变量群被称为长变量列表，由于数量较多，因此必须先检查这些变量之间的相关性。若变量间存在高度相关性，之后只要依预测能力及稳定度择一保留即可。接下来进行单因子分析，以检查各变量的预测强度。
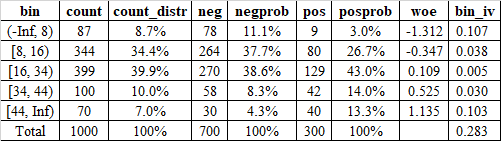
这里以一个连续型变量来做示例，一开始根据数字大小切分较细的组别。分组的原则为：
- 组间差异大，组内差异小；
- 分组占率不低于5%；
- 各组中必须同时有好样本与坏样本。
其中WoE（Weight of Evidence）称为证据权重，计算公式为：
\[WoE = \ln (\frac {Good_i} {Good_T} / \frac {Bad_i} {Bad_T}) = \ln \frac {Good_i} {Good_T} - \ln \frac {Bad_i} {Bad_T}\]negprob大于posprob时，WoE为负数，绝对值越高，表示该区间好坏样本的区隔能力越高。各组之间WoE值差距应尽可能拉开并呈现出单调的趋势。
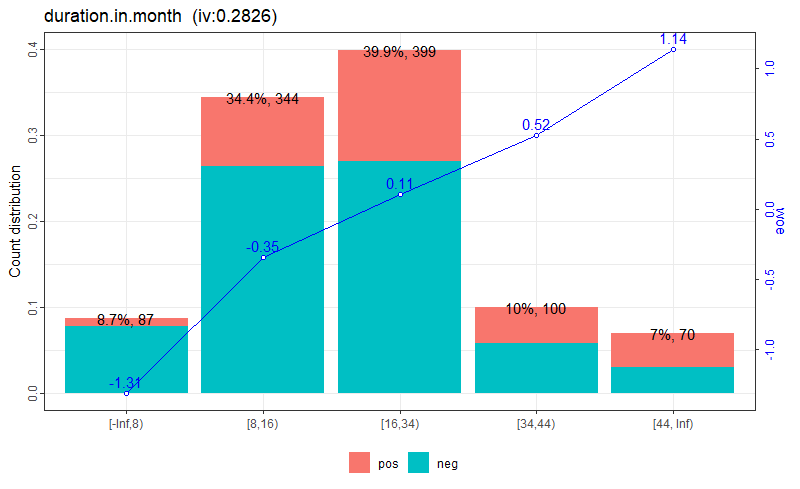
另一个重要的指标为信息量（Information Value），计算公式为：
\[IV = \sum_{i=1}^n (\frac {Good_i} {Good_T} - \frac {Bad_i} {Bad_T}) \times WoE_i\]它是每个区间上WoE的加权和，可用来表示变量预测能力的强度。
| 信息量 | 预测能力 |
|---|---|
| <0.02 | Useless |
| [0.02, 0.1) | Weak |
| [0.1, 0.3) | Medium |
| [0.3, 0.5) | Strong |
| >=0.5 | Suspicious or too good to be true |
为了使IV提高，需要调整合并WoE相近的区间，最后得到的分组结果称为粗分类。待长变量列表中的所有变量IV都计算完成后，可从中挑选变量，优先排除高度相关、趋势异常、不容易解释的。经过筛选后的变量集合称为短变量列表，即为模型的候选变量。
建立模型
理想中的信用评分模型可以将所有好坏客户划分清楚，但在实际中坏样本的比例通常很低，无法凸显风险因子的特征。因此在抽取建模样本时，会采用重抽样技术将坏样本的比例提高至正负样本的比例约为3:1~5:1。
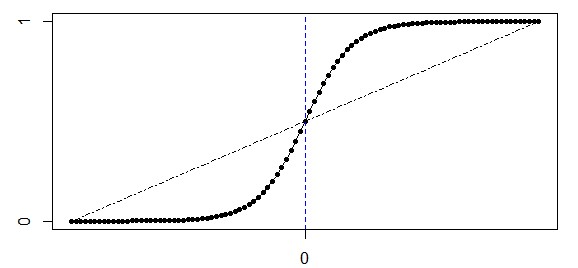
信用评分的目的是预测客户是否违约产生逾期，被解释变量是二元的。线性回归计算出的值可能会小于0或大于1，显然不合理，同时解释变量与被解释变量之间的关系是线性的，这也与生活常识不符，例如：收入很低与极低者的违约概率是很接近，收入很高与极高者的违约概率也很接近，只有中间部分的差异较大。逻辑分布的累积分布函数正好符合这个形式，即：
\[F(x; \mu, \gamma) = \frac 1 {1 + e^{- \frac {x - \mu} \gamma}}\]当$\mu = 0, \gamma = 1$时，其累积分布函数具体下面的形状，此时的函数又叫Sigmoid函数。
逻辑回归的结果是几率Odds的自然对数，若想将结果以分数形式呈现，需要进行转换：
\[Score = \ln(Odds) \times Scale + Location\]- 设定Odds=1时的分数，假设为100分；
- 设定Odds每增加一倍时增加的分数，假设为10分，此分数称为PDO（Point of Double Odds）；
- 将Odds等于1和2时的分数套入公式，得到：
解得：
\[Location = 100 \\ Scale = \frac {10} {\ln 2}\]最终公式为：
\[Score = \ln (Odds) \times \frac {10} {\ln 2} + 100\]拒绝推论
拒绝推论多用于申请评分卡。由于初步建立的模型所采用的样本皆来自核准案件，这些案件的质量相对较好，建模时若仅使用它们会造成模型的偏误。但被拒绝的部分是无法事后观测实际表现的，就无从得知有哪些案件在当时被误判，因此需要借助拒绝推论推测拒绝案件的好坏，以进行模型修正。
较常被使用的拒绝推论方法为扩充法，其概念是先以核准客户为样本建立初步模型，接着将拒绝案件套入该模型，以推测其好坏，再与原核准客户样本合并建立新的模型。
- 单纯扩充法
拒绝客户以初步模型算出违约概率，讨论一个可容忍的临界点，以此决定客户的好坏。
- 分组法
核准客户以初步模型的分数划分10~20个分组，每个分组皆可算出其正常及违约概率，拒绝客户依初步模型算出违约概率并归类至各分组中，再以该分组的正常及违约比率随机分配拒绝客户的好坏属性。
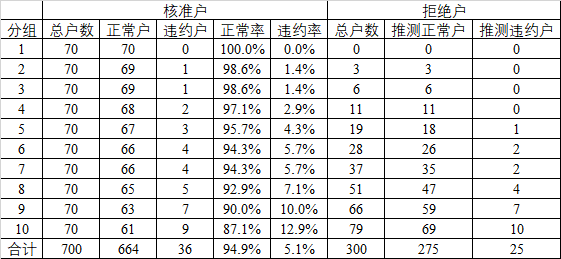
效力验证
模型建立完成后的验证可分为样本外（Out-of-Sample）验证和时间外（Out-of-Time）验证，前者使用保留样本，后者使用建模样本期外的样本。除了测试样本外，模型效力评量指针也可分为区分度与稳定度两大类。
区分度指标
区分度指模型对好坏客户的区隔能力。如果借由评分就可以精准地将好坏客户完全区分开来，那就是理想上最好的模型，但现实中不可能，模型预测出的好客户与坏客户会有一定程度的重叠。
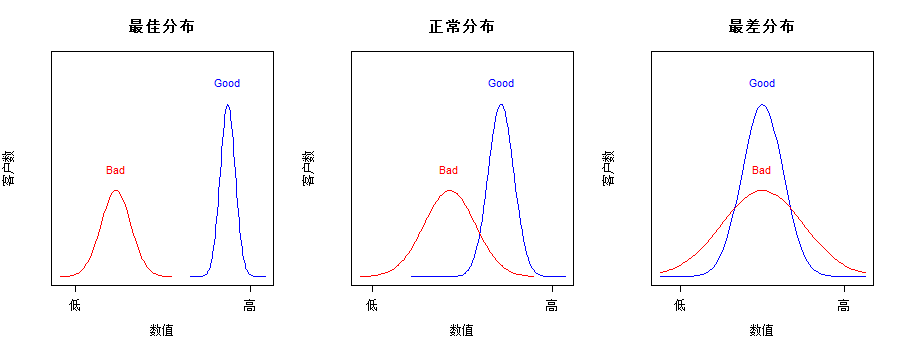
常用的区分度指标有K-S值（Kolmogrov-Smirnov）及基尼系数。
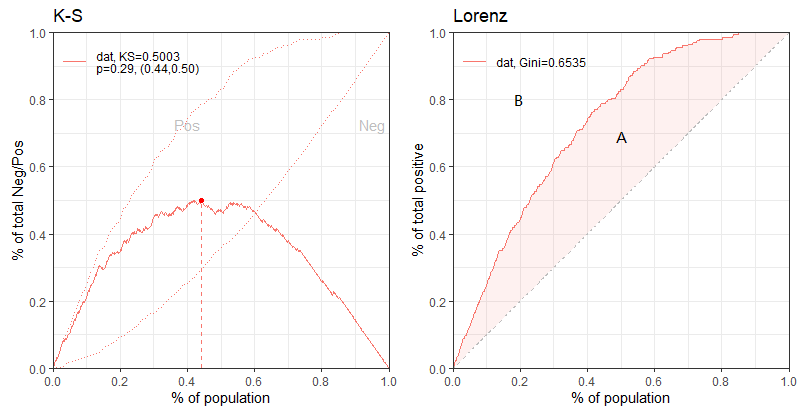
- K-S
通过衡量好坏样本的累积分布差值来评估模型的风险区分能力。
\[KS = \max (TPR - FPR)\]| K-S | 模型解释能力 |
|---|---|
| [0, 0.2) | 无 |
| [0.2, 0.3) | 可以接受 |
| [0.3, 0.5) | 较强 |
| [0.5, 0.75) | 很强 |
| [0.75, 1) | 模型可能有异常 |
- 洛伦兹曲线
纵轴为TPR，横轴为不同阈值切分下预测为正占总体的百分比。其中$45^o$线表示完全无区分能力的模型，基尼系数越大模型区分能力越强。
\[Gini = \frac A {A + B}\]稳定度指标
由于模型是特定时期的样本所开发，此模型是否适用于开发样本之外的族群，必须经过稳定性测试才能得知。稳定性指标（Population Stability Index）是验证样本（一般我们使用OOS和OOT数据）在各分数段的分布与建模样本分布的差异。
\[PSI = \sum_{i=1}^{n} (A_i - E_i) \times \ln \frac {A_i} {E_i}\]其中$A_i$表示实际占比（Actual），这里使用验证数据；$E_i$表示预期占比（Expected），这里使用建模样本。
| PSI | 模型稳定度 |
|---|---|
| [0, 0.1) | 好 |
| [0.1, 0.25) | 略不稳定 |
| [0.25, $+\infty$) | 不稳定 |
