个体与集成
集成学习通过构建多个学习器来完成学习任务,先产生一组个体学习器,再用某种策略将它们结合起来。个体学习器通常由一个现有的学习算法从训练数据产生,例如C4.5决策树、BP神经网络等。
- 集成中只包含同种类型的个体学习器时,这样的集成是同质的,同质集成中的个体学习器称为基学习器;
- 集成也可以包含不同类型的个体学习器,例如同时包含决策树与神经网络,这样的集成是异质的,这时不再有基学习器的称呼。
集成学习通过将多个学习器进行结合,常可获得比单一学习器更好的泛化性能,对于弱学习器(泛化性能略优于随机猜测)尤为明显。但一般常识下,如果把好坏不等的东西掺杂在一起,那么通常结果会是比最坏的要好一些,比最好的要坏一些。考虑一个二分类的例子,集成学习的结果通过投票法产生,实际可能会产生以下三种情况。
- 集成提升性能
| 测试例1 | 测试例2 | 测试例3 | |
|---|---|---|---|
| $h_1$ | √ | √ | × |
| $h_2$ | × | √ | √ |
| $h_3$ | √ | × | √ |
| 集成 | √ | √ | √ |
- 集成不起作用
| 测试例1 | 测试例2 | 测试例3 | |
|---|---|---|---|
| $h_1$ | √ | √ | × |
| $h_2$ | √ | √ | × |
| $h_3$ | √ | √ | × |
| 集成 | √ | √ | × |
- 集成起负作用
| 测试例1 | 测试例2 | 测试例3 | |
|---|---|---|---|
| $h_1$ | √ | × | × |
| $h_2$ | × | √ | × |
| $h_3$ | × | × | √ |
| 集成 | × | × | × |
于是我们可以得出结论:想要获得泛化性能好的集成,每个个体学习器应该要有一定的准确性,同时学习器之间要存在差异。对于一个二分类问题$y \in \lbrace-1, +1\rbrace$和真实函数$f$,假定基分类器的错误率为$\epsilon$,即对每个基分类器$h_i$有
\[P(h_i(x) \neq f(x)) = \epsilon\]假设集成通过简单投票法结合T个基分类器,集成的分类结果为
\[H(x) = sign \Bigg( \sum_{i=1}^T h_i(x) \Bigg)\]最多k个基分类器正确的概率为
\[P(H(T) \leq k) = \sum_{i=0}^k C_T^i (1 - \epsilon)^i \epsilon^{T-i}\]其中$H(T)$表示T个基分类器中分类正确的个数。假设基分类器的错误率相互独立,对于$\delta > 0$,$k = (1 - \epsilon - \delta)T$,有Hoeffding不等式(N个独立有界随机变量之和偏离该和的期望的程度是存在上界的)
\[\begin{aligned} P(H(T) \leq (1 - \epsilon - \delta)T) &= P(\frac {H(T)} T - (1 - \epsilon) \leq - \delta) \\ &\leq \exp(-2 \delta^2 T) \end{aligned}\]若有超过半数的基分类器错误,则集成分类就错误,此时的概率为
\[P(H(x) \neq f(x)) = P(H(T) \leq \frac T 2) = \sum_{i=0}^{\lfloor T/2 \rfloor} C_T^i (1 - \epsilon)^i \epsilon^{T-i}\]对应着$k = \frac T 2$,$\delta = \frac 1 2 - \epsilon$,于是
\[P(H(x) \neq f(x)) \leq \exp{\Bigg(-\frac 1 2 T (1 - 2 \epsilon) ^2\Bigg)}\]随着集成中个体分类器数目T的增大,集成的错误率将指数级下降,最终趋向于零。上面的推导中假设了基分类器的错误率相互独立,实际中个体学习器是为解决同一个问题训练出来的,它们显然不可能相互独立。个体学习器的“准确性”与“多样性”之间此消彼长,需要权衡。根据个体学习器的生成方式,目前的集成学习大致分为两类:
- 个体学习器之间存在强依赖关系,必须串行生成的序列化方法,例如Boosting;
- 个体学习器之间不存在强依赖关系,可同时生成的并行化方法,例如Bagging和随机森林。
Boosting
Boosting是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制为先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先一步基学习器做错的训练样本在后续受到更多关注,再训练下一步的基学习器,如此反复,直至基学习器数量达到事先指定的值T,最终对T个基学习器进行加权结合。
AdaBoost
AdaBoost是第一个具有适应性的算法,可以适应弱学习器各自的训练误差率,这也是其名称的由来(Adaptive)。先对每个样本赋予相同的初始权重,每一轮学习器训练过后都会根据其表现对每个样本的权重进行调整,增加分错样本的权重,这样先前做错的样本在后续就能得到更多关注,按这样的过程重复训练出T个学习器,最后进行加权组合。最后得到的强学习器为基学习器的线性组合,即加法模型
\[H(x) = \sum_{t=1}^T \alpha_t h_t(x)\]它使用的是指数损失函数
\[\ell_{exp} (H \vert \mathcal{D}) = \mathbb{E}_{x \sim \mathcal{D}} [e^{-f(x)H(x)}]\]输入:
训练集$D = {(x_1, y_1), (x_2, y_2), …, (x_m, y_m)}$;基学习算法$\mathcal{L}$;训练轮数$T$
过程:
- $\mathcal{D}_1(x) = 1/m$;
- for t = 1, 2, …, T do
- $h_t(x) = \mathcal{L}(D, \mathcal{D}_t)$;
- $\epsilon_t = P_{x \sim \mathcal{D}_t} (h_t(x) \neq f(x))$;
- if $\epsilon_t > 0.5$ then break
- $\alpha_t = \frac 1 2 \ln (\frac {1 - \epsilon_t} {\epsilon_t})$;
- $\begin{aligned} \mathcal{D}_{t+1} (x) &= \frac {\mathcal{D}_t(x)} {Z_t} \times \begin{cases} exp(-\alpha_t) &\text{if} \enspace h_t(x) = f(x) \newline exp(\alpha_t) &\text{if} \enspace h_t(x) \neq f(x) \end{cases} \newline &= \frac {\mathcal{D}_t (x) exp(-\alpha_t f(x)h_t(x))} {Z_t} \end{aligned}$
- end for
输出:$H(x) = sign (\sum_{t=1}^T \alpha_t h_t(x))$
0-1损失函数
在二分类任务中,0-1损失函数本来是最恰当的:
\[\ell(Y, f(X)) = \begin{cases} 1 & Y \neq f(X) \\ 0 & Y = f(X) \end{cases}\]但优化0-1损失函数下的目标函数,等同于直接优化分类准确率。并且它非凸、不连续,无法使用梯度下降求解,从而导致目标函数难以直接求解,这时就需要用到替代损失函数。
使用指数损失函数的原因
\[\begin{aligned} \ell_{exp} (H \vert \mathcal{D}) &= \mathbb{E}_{x \sim \mathcal{D}} [e^{-f(x)H(x)}] \\ &= e^{-H(x)} P(f(x)=1 \vert x) + e^{H(x)} P(f(x)=-1 \vert x) \end{aligned}\]若$H(x)$能使指数损失函数最小化,则对上式求关于$H(x)$的偏导并令其为零
\[\frac {\partial \ell_{exp} (H \vert \mathcal{D})} {\partial H(x)} = -e^{-H(x)} P(f(x)=1 \vert x) + e^{H(x)} P(f(x)=-1 \vert x) = 0\]于是有
\[H(x) = \frac 1 2 \ln \frac {P(f(x)=1 \vert x)} {P(f(x)=-1 \vert x)}\]换一种写法
\[P(f(x)=1 \vert x) = \frac 1 {1 + e^{-2H(x)}}\]每一轮最小化指数损失函数实际是在训练一个logistic回归模型。
\[\begin{aligned} sign(H(x)) &= sign \Bigg( \frac 1 2 \ln \frac {P(f(x)=1 \vert x)} {P(f(x)=-1 \vert x)} \Bigg) \\ &= \begin{cases} 1 & P(f(x)=1 \vert x) > P(f(x)=-1 \vert x) \\ -1 & P(f(x)=1 \vert x) < P(f(x)=-1 \vert x) \end{cases} \\ &= \mathop{\arg \max}\limits_{y \in \{-1,1\}} \quad P(f(x) = y \vert x) \end{aligned}\]这意味着$sign(H(x))$达到了贝叶斯最优错误率(为最小化总体风险,只需在每个样本上选择那个能使条件风险最小的类别标记,反映了分类器所能达到的最好性能,即通过机器学习所能产生的模型精度的理论上限)。即若指数损失函数最小化,则分类错误率也将最小化。
- 如果最优化替代损失函数的同时也最优化了原本的损失函数,则称替代损失函数具有一致性;
- 如果替代损失函数是凸函数、并且在零点可导,其导数小于0,那么它一定是具有一致性的。
因此指数损失函数是分类任务原本0-1损失函数的一致的替代损失函数。
基分类器权重的确定
在AdaBoost算法中,当基分类器$h_t$基于分布$\mathcal{D}_t$产生后,该基分类器的权重$\alpha_t$应使得$\alpha_t h_t$最小化指数损失函数
\[\begin{aligned} \ell_{exp} (\alpha_t h_t \vert \mathcal{D}_t) &= \mathbb{E}_{x \sim \mathcal{D}_t} [e^{-f(x)\alpha_t h_t(x)}] \\ &= \mathbb{E}_{x \sim \mathcal{D}_t} [e^{-\alpha_t} \Bbb{I} \big( f(x) = h_t(x) \big) + e^{\alpha_t} \Bbb{I} \big( f(x) \neq h_t(x) \big)] \\ &= e^{-\alpha_t} (1 - \epsilon_t) + e^{\alpha_t} \epsilon_t \end{aligned}\]该指数损失函数关于$\alpha_t$的一阶导数为零时取得极小值
\[\frac {\partial \ell_{exp} (\alpha_t h_t \vert \mathcal{D}_t)} {\partial \alpha_t} = -e^{-\alpha_t} (1 - \epsilon_t) + e^{\alpha_t} \epsilon_t = 0\]此时解得
\[\alpha_t = \frac 1 2 \ln \frac {1 - \epsilon_t} {\epsilon_t}\]总结
Boosting算法要求基学习器能对特定的数据分布进行学习,有两种实现方式
- 重赋权法:在训练过程的每一轮中,根据样本分布为每个训练样本重新赋予一个权重;
- 重抽样法:对应无法接受带权样本的基学习算法,在每一轮中,根据样本分布对训练集重新采样,再用重抽样过的样本集对基学习器进行训练。
一般而言,两种方法没有明显的优劣。但使用重赋权法时,如果当前训练到第t个基学习器时该学习器的错误率比不过随机猜测,则训练会在基学习器总数未达T的此时提前终止,这种情况下,集成中只包含了少量的基学习器,集成的性能大概率不佳。如果使用重抽样法,遇到某个基学习器的错误率大于50%时,可按照此时的分布重新抽样训练,从而使得学习过程可以持续到预设的T轮完成。
从偏差-方差权衡的角度看,Boosting主要关注降低偏差,因此Boosting算法可以基于泛化性能相当弱的基学习器构建出很强的集成。
Bagging与随机森林
Bagging
自助法聚集(Bootstrap Aggregating),又名Bagging,是并行集成学习方法最著名的代表。它基于自助法抽样,给定一个m个样本的数据集,我们经过m次有放回抽样,样本在m次抽样中始终不被抽到的概率是
\[\begin{aligned} \lim_{x \to \infty} (1 - \frac 1 x) ^ x &= \lim_{x \to \infty} \frac 1 {(1 + \frac 1 {x - 1}) ^ x} \\ &= \lim_{x \to \infty} \frac 1 {(1 + \frac 1 {x - 1}) ^ {x - 1}} \cdot \frac 1 {(1 + \frac 1 {x - 1})} \\ &= \frac 1 e \approx 0.368 \end{aligned}\]按照这样的方式,抽样出T个含m个样本的数据集,基于每个数据集训练一个基学习器,再将所有基学习器结合。对于分类任务,Bagging通常使用简单投票法,对于回归任务则使用简单平均法。
输入:
训练集$D = {(x_1, y_1), (x_2, y_2), …, (x_m, y_m)}$;基学习算法$\mathcal{L}$;训练轮数$T$
过程:
- for t = 1, 2, …, T do
- $h_t(x) = \mathcal{L}(D, \mathcal{D}_{bs})$;
- end for
输出:$H(x) = \mathop{\arg\max}\limits_{y \in \mathcal{Y}} \sum_{t=1}^T \Bbb{I} (h_t(x) = y)$
其中$\mathcal{D}_{bs}$是自助法抽样产生的样本分布。训练一个Bagging集成与直接训练一个基学习器的复杂度同阶,这是一个很高效的集成学习算法。与AdaBoost只适用于二分类任务不同,Bagging可用于多分类、回归任务。自助法采样使得每个基学习器只用到了初始数据集63.2%的样本,因此剩下的样本可用作验证集来对学习器的泛化性能进行包外估计(Out-of-Bag Estimate)。令$D_t$表示$h_t$实际使用的训练样本集,令$H^{oob}(x)$表示对样本x的包外预测,即仅考虑那些未使用x训练的基学习器在x上的预测,有
\[H^{oob}(x) = \mathop{\arg \max} \limits_{y \in \mathcal{Y}} \sum_{t=1}^T \Bbb{I} (h_t(x) = y) \cdot \Bbb{I} (x \notin D_t)\]于是Bagging泛化误差的包外估计为
\[\epsilon^{oob} = \frac 1 {\vert D \vert} \sum_{(x,y) \in D} \Bbb{I} (H^{oob}(x) \neq y)\]从偏差-方差权衡的角度看,Bagging主要关注降低方差,因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。
随机森林
随机森林是Bagging的一个扩展变体。RF在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树训练过程中引入了随机属性选择。每一次选择最优化分属性时,是从全属性集的一个抽样中选择,若全属性集中有d个属性,抽样需要选出k个,一般建议
\[k = \log_2 d\]RF相对于原始的Bagging进一步增加了集成中基学习器之间的差异度,这将使得最终集成的泛化性能得到提高。因为引入了属性扰动,每一个基学习器的性能往往会有所下降,因此RF的起始性能往往较差,但随着基学习器数量的增加,RF通常会收敛到相对于Bagging更低的泛化误差。并且RF因为每一轮最优化分属性的选择集缩小,使得它的训练效率要优于Bagging决策树。
结合策略
学习器结合可能会从三个方面带来好处:
- 从统计的角度,单学习器可能误选从而泛化性能不佳,结合多个学习器可以减小这一风险;
- 从计算的角度,学习算法往往会陷入局部最优,结合多个学习器可以降低陷入局部最优的风险;
- 从表示的角度,某些学习任务的真实假设可能不在当前学习算法的假设空间中,此时若使用单学习器肯定无效,通过结合多个学习器可以获得更好的近似。
对基学习器为数值型输出的集成,常用的结合策略是平均法;对基学习器为分类任务的集成,常用的结合策略是投票法;当集成中的基学习器类别不同时,可以使用Stacking方法,即通过另一个学习器来进行结合,用于结合的学习器称为次级学习器或元学习器。
Stacking先从初始数据集训练出初级学习器,然后根据初级学习器的输出当作新样本集的特征,初始数据集的标记被当作新样本集的标记,基于新样本集训练一个元学习器。
输入:
训练集$D = {(x_1, y_1), (x_2, y_2), …, (x_m, y_m)}$;基学习算法$\mathcal{L}_1, \mathcal{L}_2, …, \mathcal{L}_T$;元学习算法$\mathcal{L}$
过程:
- for t = 1, 2, …, T do
- $h_t(x) = \mathcal{L}_t(D)$;
- end for
- $D’ = \emptyset$;
- for i = 1, 2, …, m do
- for t = 1, 2, …, T do
- $z_{it} = h_t(x_i)$;
- end for
- $D’ = D’ \cup ((z_{i1}, z_{i2}, …, z_{iT}), y_i)$;
- end for
- $h’ = \mathcal{L}(D’)$;
输出:$H(x) = h’ (h_1(x), h_2(x), …, h_T(x))$
在训练阶段,次级训练集是利用初级学习器产生的,若直接用初级学习器的训练集来产生次级训练集,过拟合的风险会比较大,因此一般都是使用交叉验证或留一法这样的方式,用训练初级学习器未使用的样本来产生次级学习器的训练样本。
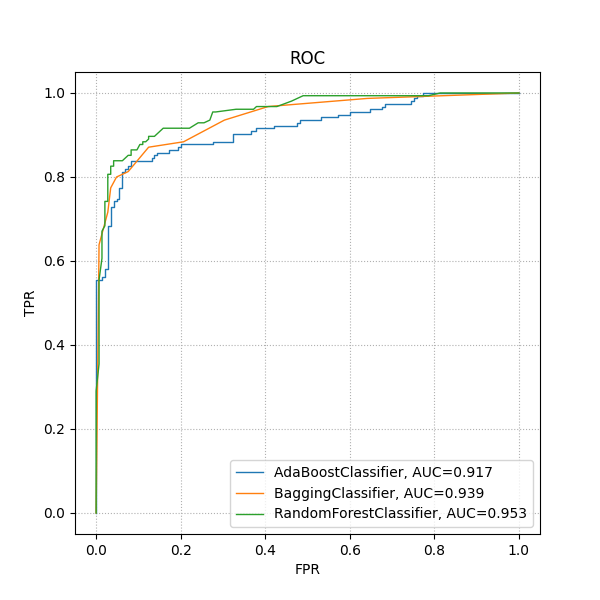
比较
from matplotlib import pyplot as plt
from sklearn.datasets import make_classification
from sklearn.ensemble import AdaBoostClassifier, BaggingClassifier, RandomForestClassifier
from sklearn.metrics import roc_curve, roc_auc_score
from sklearn.model_selection import train_test_split
X, y = make_classification(n_samples=1000, random_state=2)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.3, random_state=2)
adaboost = AdaBoostClassifier()
adaboost.fit(X_train, y_train)
bagging = BaggingClassifier()
bagging.fit(X_train, y_train)
rf = RandomForestClassifier()
rf.fit(X_train, y_train)
fig, ax = plt.subplots(figsize=(6, 6))
for clf in [adaboost, bagging, rf]:
y_pred = clf.predict_proba(X_test)[:, 1]
fpr, tpr, thresholds = roc_curve(y_test, y_pred)
auc = roc_auc_score(y_test, y_pred)
ax.plot(fpr, tpr, label=f'{str(clf).strip("()")}, AUC={round(auc, 3)}', linewidth=1)
ax.legend()
ax.grid(axis='x', linestyle=':')
ax.grid(axis='y', linestyle=':')
ax.set_xlabel('FPR')
ax.set_ylabel('TPR')
ax.set_title('ROC')
fig.savefig('result.png', transparent=True)
plt.close(fig)